
Local dos seminários: sala 6.2.33 | Entrada Livre
16 de julho
(9h30) Receção
Sala 6.2.33
+
Projeto
+
(16h) Seminário
"O que é um computador?", por Bruno Loff
(seguido de coffee-break)
17 de julho
Projeto
+
(16h) Seminário
Da construção geométrica de fractais à identificação de padrões fractais em dados reais,
por Cristina Serpa
(seguido de coffee-break)
18 de julho
Projeto
+
(15h) Workshop
Comunicar ciência: boas práticas para uma comunicação eficaz, por Marta Santos
(seguido de coffee-break)
19 de julho
Projeto
+
(16h) Seminário
Some examples of moduli spaces of curves,
por Giosuè Muratore
(seguido de coffee-break)
22 de julho
Projeto
+
(16h) Seminário
O Mathematica, uma ferramenta computacional,
por Pedro Duarte
(seguido de coffee-break)
23 de julho
Projeto
+
(16h) Seminário
"Uma viagem pelas funções geradoras através da Álgebra de Weyl",
(seguido de coffee-break)
24 de julho
Projeto
+
(16h) Seminário
A Hipótese de Riemann aos 165 anos,
por Jorge Buescu
(seguido de coffee-break)
25 de julho
Projeto
+
(16h) Seminário
A glimpse into the dark side of partial differential equations and beyond, por Jean-Baptiste Casteras
(seguido de coffee-break)
26 de julho
Projeto
+
(14h) Apresentação dos projetos
(seguido de coffee-break)
Programa das Apresentações dos Projetos
-
14h Entrega dos certificados
-
14h15 Joana Carreira Ventura (LM)
Título: O problema das 8 rainhas
Mentora: Maria Osório
14h30 João Martins (LF)
Título: Física dos Números
Mentor: João Fontinha
14h45 Leonor Sofia Bernardo (LF)
Título: Asymptotic Analysis of ODEs
Mentor: Gabriele Degano
15h Sara Oliveira (LF)
Título: Beth Ansatz - The Heisenberg Model
Mentor: Gabriele Degano
15h15 Tiago Barradas (LF)
Título: Recorrência
Mentor: Tomé Graxinha
-
15h30 Beatriz Silva (LMA)
Título: Modelos Matemáticos em Epidemiologia: Discreto versus Contínuo
Mentora: Diana Ferreira
15h45 Lucas Sinkovec (LMA)
Título: Como jogar Hex num toro?
Mentor: Guilherme Velez
16h Eduardo Soares (LM)
Título: O milagre da multiplicação
Mentor: Pedro Campos
16h15 Lourenço Entrudo (LF)
Título: Nem tudo o que é patológico se joga fora: dimensão e cálculo fractal
Mentor: Guilherme Velez
16h30 Intervalo com Coffee-break (20 minutos)
-
16h50 Carlos Mendes (LM)
Título: The Trillion Dollar Equation
Mentor: Pedro Campos
17h05 Ruben Martinho (LM)
Título: Funções quase-periódicas e Aplicações a Equações Diferenciais com Atrasos
Mentor: Rodrigo Luís
17h20 Manuel Madelino (LM)
Título: Um modelo para dinâmica de discussões
Mentor: Duarte Costa
17h35 Roy Lowe (LM)
Título: O Teorema dos Números Primos
Mentor: Tomé Graxinha
17h50 Ana Leonor Nunes (LF)
Título: Teorema de Kleene: Autómatos e Linguagens
Mentor: Diogo Abreu
-
18h05 Francisco Silva (LF)
Título: Teoria de Twistors e a Equação de Airy
Mentor: Tomás Inácio
18h20 Rui Rodrigues (LM)
Título: Semigrupos Inversos?
Mentora: Ana Catarina Monteiro
18h35 Kostiantyn Kostiuk (LM)
Título: Para além dos grupos
Mentora: Ana Catarina Monteiro
18h50 Encerramento seguido de lanche
Data: 16 de julho
Título: O que é um computador?
Orador: Bruno Loff
Resumo:
Estão por todo o lado, na secretária, no bolso, na máquina de lavar, mas o que são, exactamente, os computadores?
O computador é o objecto humano mais matemático que existe. Um computador é uma máquina para fazer contas. O computador foi inventado em 1936, por um matemático chamado Alan Turing, muitos anos antes de existir tecnologia que permitisse construir um.
Vou falar um bocadinho da história do computador, descrever a definição original do Turing, e explicar como é que ela se assemelha aos computadores modernos.

Data: 17 de julho
Título: Da construção geométrica de fractais à identificação de padrões fractais em dados reais
Orador: Cristina Serpa
Resumo:
Os fractais são estruturas que desafiam a forma de pensar a geometria. Não têm uma definição única e são fáceis de obter a partir de uma configuração inicial e de uma regra de construção. Encontram-se vários exemplos na natureza de forma muito diversificada. O desenvolvimento teórico é muito exigente, mas permitiu obter uma ferramenta importante em aplicações para identificar padrões fractais em dados reais. Para além de ser possível medir a estrutura fractal é ainda possível estimar funções fractais que aproximam a estrutura de uma sequência de números. Esta é uma técnica muito recente e está a começar a ser implementada em algumas áreas científicas, tais como, os materiais, a biologia, a medicina e a economia.

Data: 18 de julho
Título: Comunicar ciência: boas práticas para uma comunicação eficaz
Orador: Marta Daniela Santos
Resumo:
A ciência está cada vez mais presente no nosso dia-a-dia. E os cientistas têm a responsabilidade de ter uma voz ativa em comunicar este conhecimento.
Neste workshop vamos explorar por que é importante para os cientistas comunicarem ciência e que boas práticas podem ser utilizadas para comunicar conceitos científicos, que podem ser complexos, de forma mais clara e cativante.

Data: 19 de julho
Título: Some examples of moduli spaces of curves
Orador: Giosuè Muratore
Resumo:
A moduli space is a topological space whose points parameterize all objects of a certain family. They are very common in modern algebraic geometry.
In enumerative geometry, the solution of an enumerative problem is often obtained as the intersection of subvarieties of a proper moduli space. Moreover, moduli spaces arise naturally in various areas of physics, such as string theory and theoretical physics.
We show some examples of moduli spaces of curves, highlighting their role in classification problems.
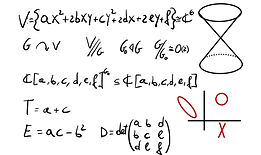
Data: 22 de julho
Título: O Mathematica, uma ferramenta computacional
Orador: Pedro Duarte
Resumo:
Precisa de uma ferramenta computacional para resolver automaticamente uma certa classe de problemas ou para executar automaticamente um determinado tipo de tarefa?
Se os Motores de Busca e a Inteligência Artificial não lhe derem rapidamente a solução de que precisa muito provavelmente terá de escrever o seu próprio código.
Nesse sentido os Sistemas de Computação Algébrica (CAS na sigla Inglesa) são Linguagens de Programação especialmente vocacionadas para as necessidades computacionais em Matemática (e.g., Cálculo Numérico e Simbólico, Representação Gráfica, Edição de Texto e de Imagem) que incorporam bibliotecas gigantescas de recursos computacionais pré-definidos.
Através de alguns exemplos de criação de ferramentas personalizadas vou ilustrar como o Mathematica, que é um CAS específico desenvolvido pela Wolfram, pode ser usado como uma ferramenta versátil e poderosa tanto no Ensino como na Investigação em Matemática.

Data: 23 de julho
Título: Uma viagem pelas funções geradoras através da Álgebra de Weyl
Orador: Maria Manuel Torres
Resumo:
Uma função geradora é uma série de potências cujos coeficientes são os termos de uma sucessão numérica. Iremos mostrar que a acção da álgebra de Weyl sobre algumas funções geradoras famosas permite obter generalizações de identidades clássicas, nomeadamente da fórmula de Dobinski para os números de Bell e da igualdade de Worpitzky que envolve os números binomiais e os números eulerianos. Pelo caminho iremos também encontrar os números de Stirling de segunda espécie e os diagramas de Young.

Data: 24 de julho
Título: A Hipótese de Riemann aos 165 anos
Orador: Jorge Buescu
Resumo:
A Hipótese de Riemann afirma que os zeros da função Zeta estão na recta vertical Re(z)=1/2 . Este é talvez o mais importante, e seguramente o mais famoso, problema em aberto na Matemática. Tem implicações extraordinárias, a primeira das quais – que levou à sua introdução por Riemann – é que a distribuição dos números primos tem um equilíbrio óptimo entre aleatoriedade e regularidade. Num sentido matematicamente preciso, à la Fourier, a Hipótese de Riemann assegura a harmonia da música dos primos.
Para além disso, tem impacto em muitas outras áreas: há dezenas de resultados demonstrados supondo que a Hipótese de Riemann é verdadeira. Por outro lado, ela admite generalizações formalmente análogas a outros contextos, como L-funções de Dirichlet ou L-funções automórficas. Saber se a HR é verdadeira nesses contextos teria implicações profundas.
Mas para isso teríamos de saber se a Hipótese de Riemann básica é ou não verdadeira. E até hoje, apesar de enormes esforços de grandes matemáticos (e do Prémio do Milénio, de um milhão de dólares) a Hipótese de Riemann continua… uma hipótese.

Data: 25 de julho
Título: A glimpse into the dark side of partial differential equations and beyond
Orador: Jean-Baptiste Casteras
Resumo:
Partial differential equations (PDEs) are ubiquitous mathematical objects to model real-world phenomena. They are the keystone of the modern understanding of sound and heat propagation, population dynamics, fluid dynamics, general relativity and quantum mechanics among other fields. They also arise from many purely mathematical subjects such as differential geometry or calculus of variations. In this talk, I will focus on the Schrödinger equation. This is one of the basic examples of a class of PDEs called dispersive. I will try to give a gentle introduction on this very vast topic.
